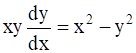
Given Differential equation is:

⇒

⇒ ……(1)

Homogeneous equation: A equation is said to be homogeneous if f(zx,zy) = zⁿf(x,y) (where n is the order of the homogeneous equation).

Let us assume

⇒

⇒

⇒

⇒

⇒ f(zx,zy) = z⁰f(x,y)

So, given differential equation is a homogeneous differential equation.

We need a substitution to solve this type of linear equation and the substitution is y = vx.

Let us substitute this in (1)

⇒

We know that

⇒

⇒

⇒

⇒

⇒

⇒

Bringing like on the same side we get,

⇒

⇒

⇒

We know that

Integrating on both sides we get,

⇒

⇒

(∵ logC is an arbitrary constant)

⇒ log(1-2v²) = -4logx + 4logC

⇒ log(1–2v²) = -logx⁴ + logC⁴

(∵ xloga = loga^x)

⇒

(∵ )

Applying exponential on both sides we get,

⇒

Since y = vx, we get,

⇒

⇒

⇒

⇒

Cross multiplying on both sides we get,

⇒ x²(x²–2y²) = c⁴

⇒ x⁴–2x²y² = c⁴

∴ The solution for the given differential equation is x⁴–2x²y² = C⁴.