Given Differential equation is:

⇒

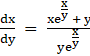⇒ ……(1)

Homogeneous equation: A equation is said to be homogeneous if f(zx,zy) = zⁿf(x,y) (where n is the order of the homogeneous equation).

Let us assume:

⇒

⇒

⇒

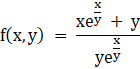
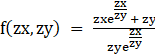
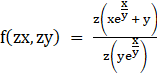
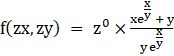
⇒ f(zx,zy) = z⁰f(x,y)

So, given differential equation is a homogeneous differential equation.

We need a substitution to solve this type of linear equation and the substitution is x = vy.

Let us substitute this in (1)

⇒

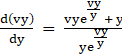
We know that:

⇒

⇒

⇒

⇒

Bringing like variables on the same side we get,

⇒

We know that ∫e^xdx = e^x + C and

Integrating on both sides, we get,

⇒

⇒ e^v = logy + C

Since x = vy, we get

⇒

∴ The solution for the given Differential equation is .