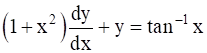
(i) If a differential equation is ,

then y(I.F) = ∫Q.(I.F)dx + c, where I.F = e^∫Pdx

Given:-

This is a linear differential equation, comparing it with

I.F = e^∫Pdx

Solution of the equation is given by

y(I.F) = ∫Q.(I.F)dx + c

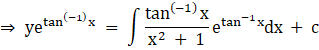
let tan^–1x = t

so, ye^t = –∫te^t dt + c

= t∫ e^t dt–∫( e^t dt)dt + c

using integration by parts

y e^t = te^t –e^t + c

⇒ y = (t–1)ce^–t