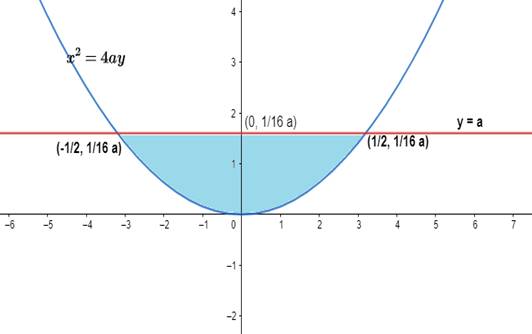
Find the area of the region bounded by x2 = 4ay and its latus rectum.
This is a simple problem of the area under the two curves.
Step 1: Find the latus rectum and its intersection points with the parabola.
![]()
![]()
Comparing it with the standard form of a parabola
Y = 4 A x2
Where (0, A) is the coordinate of the focus of the parabola. And the latus rectum passes through this point and is perpendicular to the axis of symmetry.
Therefore, the equation of latus rectum is y = a.
Comparing equation (1) and (2)
![]()
![]()
![]() The equation of the latus rectum:
The equation of the latus rectum:
![]()
Intersection points
![]()
![]()
![]()
Step 2: Integrating the expression to find the area enclosed by the curves.
Since the latus rectum is above the parabola in the cartesian plane, the expression will be:
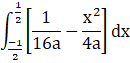
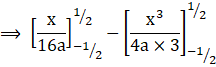
![]()
![]()
3