The given equations are,

y² = 6x

And x^{2 =} 6y.

When y = 0 then x = 0,

Or

Putting x value on y² = 6x,

y² = 6

Or 6

Or

Or y = 6

When y = 0 then x = 0,

And When y = 6 then x = 6,

On solving these two equations, we get point of intersections.

The points are O (0,0) and A(6,6). These are shown in the graph below

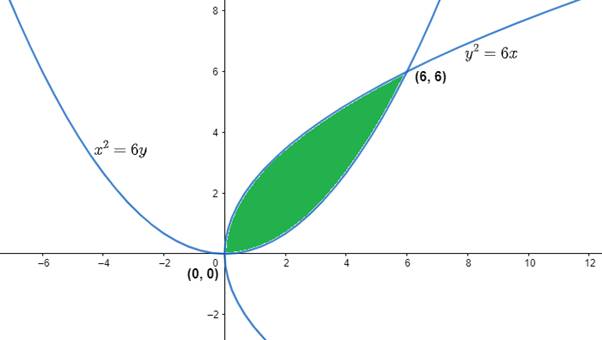
Now the bounded area is the required area to be calculated, Hence,

Bounded Area, A = [Area between the curve (i) and x axis from 0 to 6] - [Area between the curve (ii) and x axis from 0 to 6]

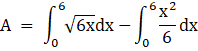
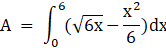
On integrating the above definite integration,

Area of the region bounded by the parabolas y² = 6x and x^{2 =} 6y is 12sq. units.