The given equations are,

Y = 4 – x² ...(i)

Y = 0 ...(ii)

And y = 3 ...(iii)

Equation (i) represents a parabola with vertex (0,4) and passes through (0,2),(0,02)

Equation (ii) is x - axis and cutting the parabola at C (2, 0)and D( – 2,0)

Equation (iii) is a line parallel to x - axis cutting the parabola at A(3,1)and B( – 3,1)

On solving these equations, we get point of intersections.

The points of intersections of a parabola with the other two lines are A(3,1), B( – 3,1), C(2,0) and D( – 2,0). These are shown in the graph below

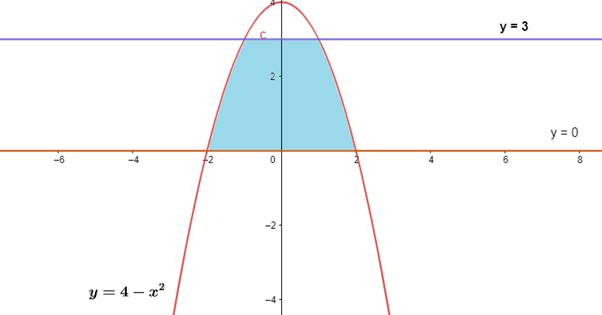
Now the bounded area is the required area to be calculated,

Hence, Bounded Area, A = 2 times [Area between the equation (i) and y axis from y = 0 to y = 3]

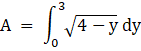
On integrating the above definite integration,

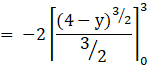
The area bounded by the curve y = 4 – x² and the lined y = 0, y = 3 is .