There are two equations involved in the question,

Represents an ellipse, symmetrical about both axis and cutting x - axis

at B (a,0) and ( – a,0)

Represents the area inside the ellipse

Represents a straight line cutting x - axis at B(a,0)

Represents the area above the straight line.

Form the given these two equations; we get the point of intersections. The points are B(a,0) and A(0,b). These are shown in the graph below

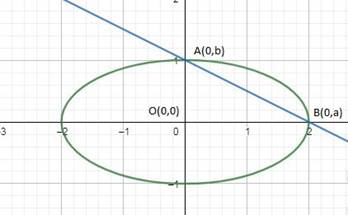
The common area is the smaller area of an ellipse.

A = [Area between the curve (i) and x axis from 0 to a] – [Area between the curve (ii) and x axis from 0 to a]

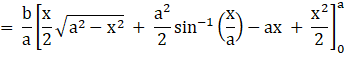
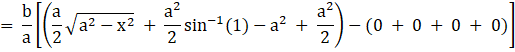
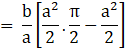
SO, the required area is square units.