To find the area of the triangular region bounded by

y = 2x + 1 (Say, line AB) ...(i)

y = 3x + 1 (Say, line BC) ...(ii)

y = 4 (Say, line AC) ...(iii)

The sketch of the curves are drawn below,

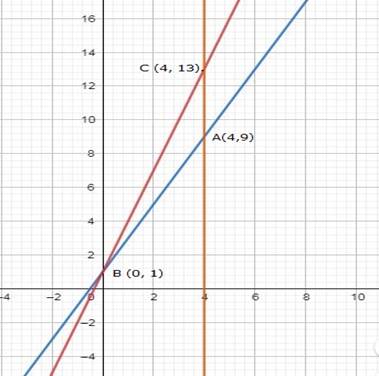
Equation (i) represents a line passing through points B(0,1) and ,

Equation (ii) represents a line passing through (0,1) and .

Equation (ii) represents a line parallel to y - axis passing through (4, 0).

Solving equation (i) and (ii) gives point B (0, 1).

Solving equation (ii) and (iii) gives point C (4, 13).

Solving equation (i) and (iii) gives point A (4, 9).

So, the Required area, A = (Region ABCA) = [Area between line BC and x - axis from x = 0 to x = 4] - [Area between line AB and x - axis from x = 0 to x = 4]

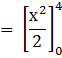
= 8 sq.units

So the Required area is 8 sq. units.