There are two equations,

x² + y² = 16 ...(i)

y² = 6x ...(ii)

From (i) and (ii)

X² + 6x = 16

Or, X² + 6x – 16 = 0

Or, (x + 8)(x – 2) = 0

Or, x = – 8 or x = 2

And when x = 2 then y = ±2√3

Equation (i) represents a circle with centre (0,0) and radius 4 units, so it meets x - axis at (±4,0) and equation (ii) represents a parabola with vertex (0,) and axis as x - axis

Points of intersection of parabola and circle are (2,2√3) and (2, – 2√3).

The sketch of the two curves are drawn below,

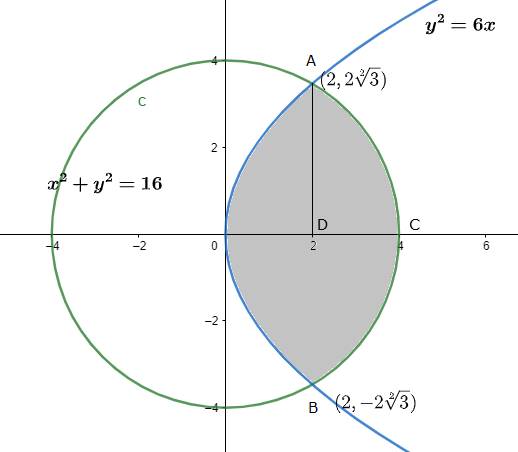
The shaded region represents the required area.

Required area = Region OBCAO

Required area = 2 (region ODAO + region DCAD)

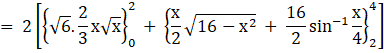
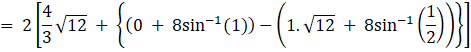
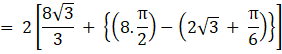
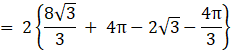
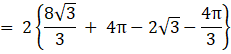
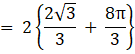
So, the required area is sq units.