To find region enclosed by

y² = x ...(i)

And x + y = 2 ...(ii)

From equation (i) and (ii),

y² + y – 2 = 0

Or, (y + 2) (y – 1) = 0

Or, y = – 2, 1

x = 4,1

Equation represents a parabola with vertex at origin and its axis as x - axis

Equation represents a line passing through (2,0) and (0,2)

On solving these two equations, we get point of intersections. The points of intersection of line and parabola are (1,1) and (4, – 2) These are shown in the graph below

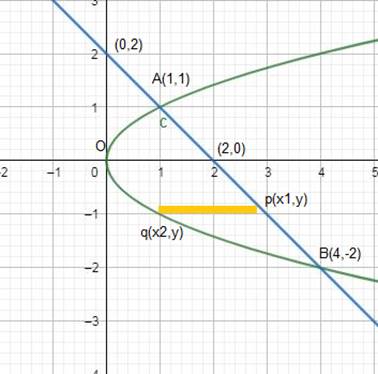
Shaded region represents the required area. We slice it in rectangles of width Δy and length = (x₁ – x₂).

Area of rectangle = (x₁ – x₂)Δy.

Required area of Region AOBA

The area of the region included between the parabola y² = x and the line x + y = 2.

is