To find the area bounded by

y² = 4x

...(i)

And x² = 4y

...(ii)

On solving the equation (i) and (ii),

= 4x

Or, x⁴ – 64x = 0

Or, x(x³ – 64) = 0

Or, x = 0, 4

Then y = 0,4

Equation (i) represents a parabola with vertex (0,0) and axis as x – axis. Equation (ii) represents a parabola with vertex (0,0) and axis as y - axis.

Points of intersection of the parabola are (0,0) and (4,4).

A rough sketch is given as: -

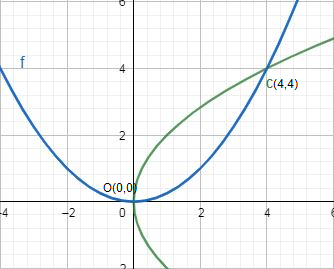
Now the bounded area is the required area to be calculated, Hence,

Bounded Area, A = [Area between the curve (i) and x axis from 0 to 4] – [Area between the curve (ii) and x axis from 0 to 4]

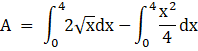
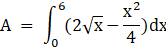
On integrating the above definite integration,

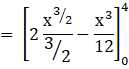
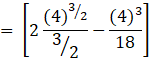
Area of the region bounded by the parabolasy² = 4x and x² = 4y is sq. units.