Book: RD Sharma - Mathematics (Volume 2)
Chapter: 21. Areas of Bounded Regions
Subject: Maths - Class 12th
Q. No. 16 of Exercise 21.3
Listen NCERT Audio Books to boost your productivity and retention power by 2X.
Find the area included between the parabolasy2 = 4ax and x2 = 4by.
To find area enclosed by
Y2 = 4ax
...(i)
And X2 = 4by
...(ii)
On solving the equation (i) and (ii),
Or, x4 – 64ab2x = 0
Or, x(x3 – 64ab2) = 0
Or, x = 0 and x = 
Then y = 0 and y = 
Equation (i) represents a parabola with vertex (0,0) and axis as x–axis,
Equation (ii) represents a parabola with vertex (0,0) and axis as x - axis,
Points of intersection of parabolas are O (0,0) and 
These are shown in the graph below: -
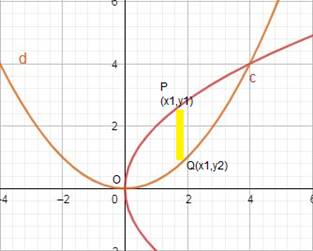
The shaded region is required area, and it is sliced into rectangles of width and length (y1 – y2)ΔX.
This approximation rectangle slides from
x = 0 to 
, so
Required area = Region OQCPO
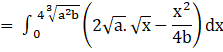
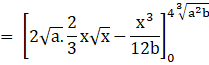
The area included between the parabolasy2 = 4ax and x2 = 4by is 
