Prove that the area in the first quadrant enclosed by the axis, the line x = √3y and the circle x 2 + y 2 = 4 is π /3.

Question

Philoid · Accepted Answer

To find an area in the first quadrant enclosed by the x – axis,

x = √3y

x² + y² = 4

Or

And

Equation (i) represents a line passing through (0,0), ( – √3, – 1), (√3,1).

Equation (ii) represents a circle centre (0,0) and passing through (±2,0), (0,±2).

Points of intersection of line and circle are ( – √3, – 1) and (√3,1).

These are shown in the graph below: -

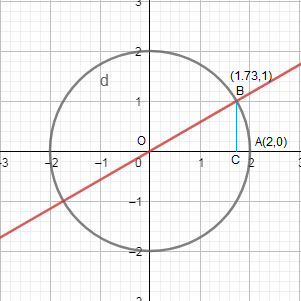
Required enclosed area = Region OABO

= Region OCBO + Region ABCA

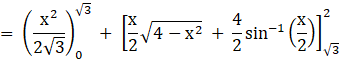
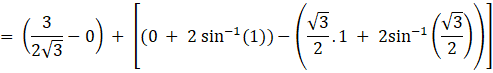
Hence proved that the area in the first quadrant enclosed by the axis, the line and the circle is π/3.