Find the area common to the circle x 2 + y 2 = 16 a 2 and the parabola y 2 = 6ax. OR Find the area of the region {(x,y):y 2 ≤ 6ax} and {(x,y):x 2 + y 2 ≤ 16a 2 }.

Question

Philoid · Accepted Answer

To find area given equations are

y² = 6ax ...(i)

x² + y² = 16 a² ...(ii)

On solving Equation (i) and (ii)

Or x² + (6ax)² = 16a²

Or x² + (6ax)² – 16a² = 0

Or (x + 8a) (x – 2a) = 0

Or x = 2a or x = – 8a is not possible solution.

Then y² = 6a(2a) = 12a² = 2√3a

Equation (i) represents a parabola with vertex (0,0) and axis as x - axis.

Equation (ii) represents a with centre (0,0) and meets axes (±4a,0), (0,±4a).

Point of intersection of circle and parabola are (2a,2√3a), (2a, – 2√3a).

These are shown in the graph below: -

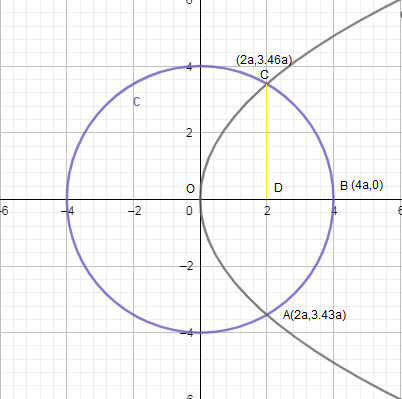
Required area = 2[Region ODCO + Region BCDB]

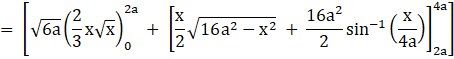
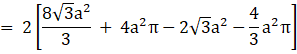
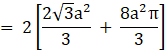
The area common to the circlex² + y² = 16 a² and the parabola y² = 6ax is

Find the area common to the circle x2 + y2 = 16 a2 and the parabola y2 = 6ax.ORFind the area of the region {(x,y):y2 ≤ 6ax} and {(x,y):x2 + y2 ≤ 16a2}.

Find the area common to the circle x² + y² = 16 a² and the parabola y² = 6ax.
OR

Find the area of the region {(x,y):y² ≤ 6ax} and {(x,y):x² + y² ≤ 16a²}.