To find area lying above x - axis and included in the circle

x² + y² = 8x ...(i)

Or (x – 4)² + y² = 16

And ...(ii)

On solving the equation (i) and (ii),

x² + y² = 8x

Or x² – 4x = 0

Or x(x – 4) = 0

Or x = 0 and x = 4

When x = 0, y = 0

When x = 4, y = ±4

Equation (i) represents a circle with centre (4,0) and meets axes at (0,0) and (8,0).

Equation (ii) represent a parabola with vertex (0,0) and axis as x - axis.

They intersect at (4, – 4) and (4,4).

These are shown in the graph below: -

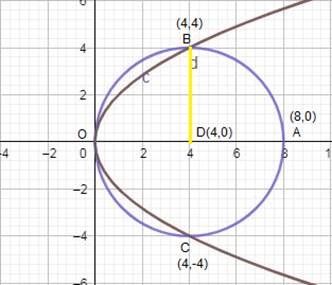
Required area = Region OABO

Required area = Region ODBO + Region DABD …(1)

Region ODBO

Region OBDO = 32/3 sq. units …(2)

Region DABD

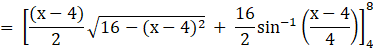
Region DABD = 4π sq. units …(3)

Using (1),(2) and (3), We get

Required area =

= 4 sq. units

The area lying above the x - axis and included between the circle x² + y² = 8x and the parabola y² = 4x is 4 sq. Units