To find the area enclosed by

y = √3x ...(i)

x² + y² = 16 ...(ii)

On solving the equation (i) and (ii),

Or x² + = 16

Or 4x² = 16

Or x² = 4

Or x =

∴ Y = ±

Equation (i) represents a parabola with vertex (0,0) and axis as x - axis.

Equation (ii) represent axis a circle with centre (4,0) and meets axes at (0,0) and (4,0).

They intersect at A (2,) and C ( – 2, – ).

These are shown in the graph below: -

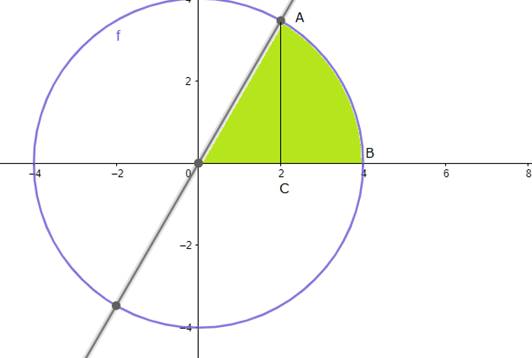
Area of the region OAB = Area OAC + Area ACB

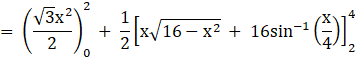
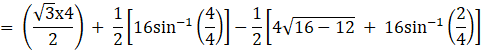
The area of the region in the first quadrant enclosed by x - axis, the line y = √3x and the circle x² + y² = 16 is