To find area bounded by

y² = 2x + 1 ...(i)

X – y – 1 = 0. ...(ii)

On solving the equation (i) and (ii),

X – y = 1

Or y² = 2(y – 1) + 1

Or y² = 2y – 1

Or (y + 1)(y – 3) = 0

Or y = 3 or – 1

∴ x = 4,0

Equation (i) is a parabola with vertex and passes through (0, 1), A (0, – 1)

Equation (ii) is a line passing through (1, 0) and (0, – 1).

Points of intersection of parabola and line are B (4, 3) and A (0, – 1)

These are shown in the graph below: -

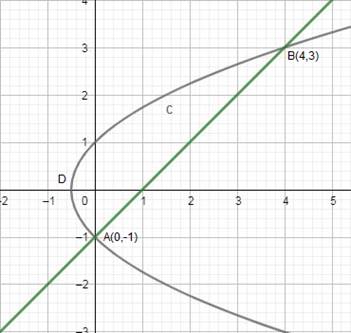
Required area = Region ABCDA

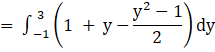
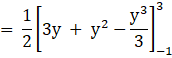
Area of the region bounded by the parabola y² = 2x + 1 and the line x – y – 1 = 0is .