To find region enclosed by

3x – y – 3 = 0 ...(i)

2x + y – 12 = 0 ...(ii)

x – 2y – 1 = 0 ...(iii)

Solving (i) and (ii), we get,

5x – 15 = 0

Or x = 3

∴y = 6

The points of intersection of (i) and (ii) is B (3,6)

Solving (i) and (iii), we get,

5x = 5

Or x = 1

∴y = 0

The points of intersection of (i) and (iii) is A (1,0)

Solving (ii) and (iii), we get,

5x = 25

Or x = 5

∴y = 2

The points of intersection of (ii) and (iii) is C (5,2) .

These are shown in the graph below: -

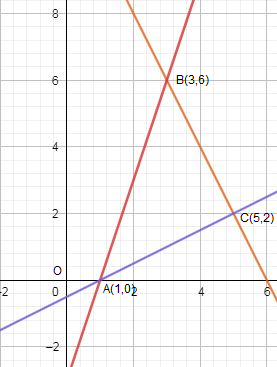
Area of the bounded region

=

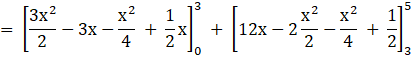
= 11 sq. units

The area of the region bounded by the following line 3x – y 3 = 0, 2x + y – 12 = 0, x – 2y – 1 = 0 is