To find area of region

{(x,y)|x – 1|≤y≤√5 – x²}

|x – 1| = y

And x² + y² = 5 …(iii)

|x – 1|≤y≤√5 – x²

|x – 1| = √5 – x²

X = 2, – 1

Equation (i) and (ii) represent straight lines and equation (iii) is a circle with centre (0,0), meets axes at (±√5,0) and (0,±√5).

These are shown in the graph below: -

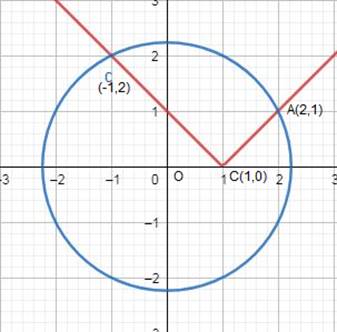
Required area = Region BCDB + Region CADC

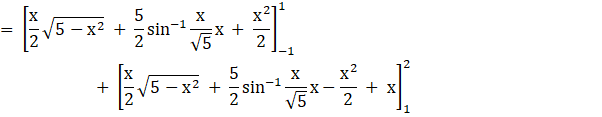
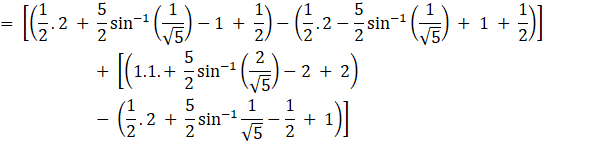
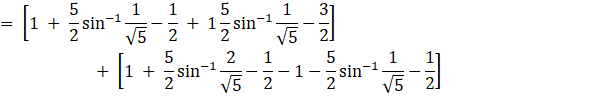
The area of the region {(x,y)|x – 1|≤y≤√s – x²} is