To find are bounded by

Y = |x – 1|

y = 1

y = x – 1

or, 1 = x – 1

or, x – 2 = 0

or, x = 2

C(2,1) is point of intersection of y = x – 1 and y = 1.

y = 1 – x

1 = 1 – x

X = 0

A(0,1) is point of intersection of y = 1 – x and y = 1.

Points of intersection are A (0, 1) and C(2,1)

These are shown in the graph below: -

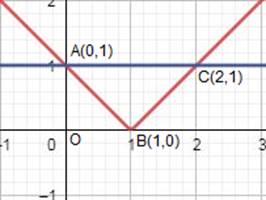
Required area = Region ABCA

= Region ABDA + Region BCDB

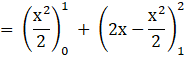
= 1 sq. units

The area of the region bounded by y = |x – 1| and y = 1 is