To find area of in first quadrant enclose by the circle

X² + y² = 32 …(i)

And y = x …(ii)

Solving these two equations, we get

Or 2X² = 32

Or X² = 16

Or x = 4

∴y = 4

Equation (i) is a circle with centre (0, 0) and meets axes at A (±4√2, 0), (0,±4√2). And y = x is a line passes through (0, 0) and intersect circle at B (4, 4).

These are shown in the graph below:

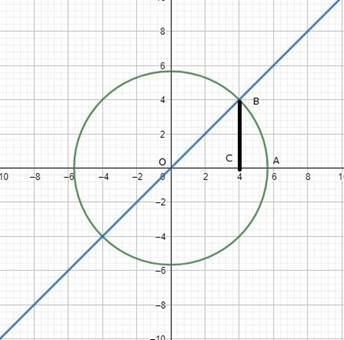
Region OABO = Region OCBO + Region CABC

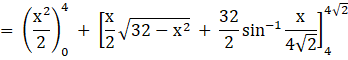
The area of the region bounded by y = x and circle X² + y² = 32 is