Find the area of the circle x2 + y2 = 16 which is exterior the parabola y2 = 6x.
The given equations are
x2 + y2 = 16 …(i)
And y2 = 6x …(ii)
On solving the equation (i) and (ii),
Or x2 + 6x = 16
Or x2 + 6x – 16 = 0
Or (x + 8)(x – 2) = 0
Or x = 2 or – 8 is not possible solution
∴ When x = 2, y = ±![]() = ±
= ±![]() = ±
= ±![]()
Equation (i) is a circle with centre (0, 0) and meets axes at (±4,0), (0,±4)
Equation (ii) represents a parabola with axis as x - axis.
Points of intersection are A (![]() ) and C (2,
) and C (2,![]() )
)
These are shown in the graph below:
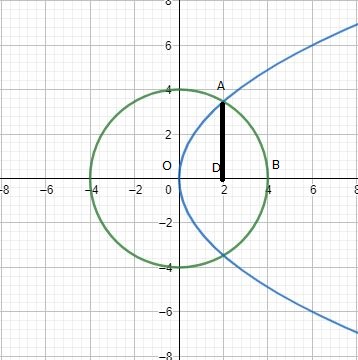
Area bounded by the circle and parabola
= 2[Area (OADO) + Area (ADBA)]
![]()
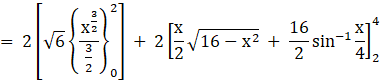
![]()
![]()
![]()
![]()
![]()
![]()
Area of circle = π(r) 2
= π(4)2
= 16π sq. Units
Thus, required area![]()
![]()
![]()
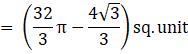
The area of the circle x2 + y2 = 16 which is exterior the parabola y2 = 6x is
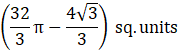
37