To find area given equations are

Y = x² + 3 …(i)

Y = 2x + 3 …(ii)

And x = 3 …(iii)

Solving the above three equations to get the intersection points,

x² + 3 = 2x + 3

Or x² – 2x = 0

Or x(x – 2) = 0

And x = 0 or x = 2

∴ y = 3 or y = 7

Equation (1) represents a parabola with vertex (3, 0) and axis as y – axis.

Equation (2) represents a line a passing through (0, 3) and ( – 3/2, 0)

The points of intersection are A (0,3) and B(2,7).

These are shown in the graph below:

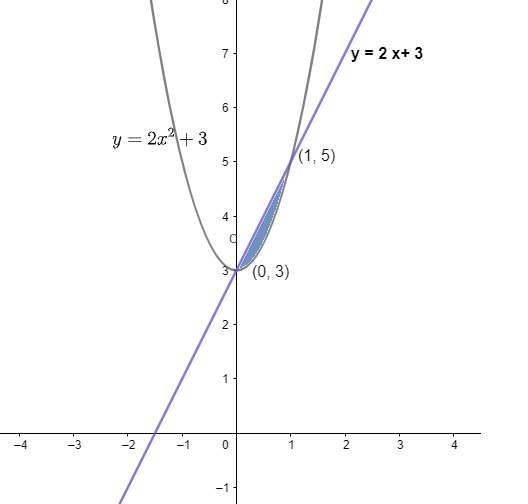
Required area =

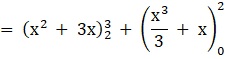
The area of the region{(x,y): 0≤y≤x² + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} is