To find the area bounded by

Y = 4x + 5 (Say AB) …(i)

Y = 5 – x (Say BC) (ii)

4y = x + 5 (Say AC) ...(iii)

By solving equation (i) and (ii), points of intersection is B (0, 5)

By solving equation (ii) and (iii), points of intersection is C (3, 2)

By solving equation (i) and (iii), we get points of intersection is A ( – 1, 1)

These are shown in the graph below:

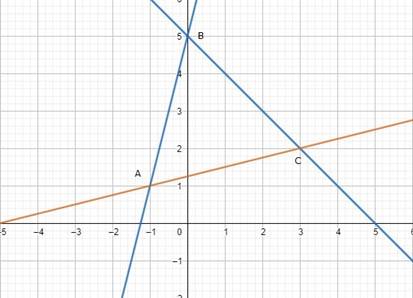
Required area = area of (ΔABD) + area of (ΔBDC) …(1)

Area of (ΔABD) =

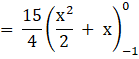
…(2)

Area of (ΔBDC) =

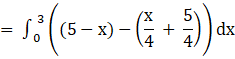
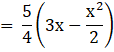
Area of (ΔBDC) = …(3)

Using equation (1), (2) and (3)

Required area = Area (ΔABD) + Area (ΔBDC)

Required bounded area of = Area of (ΔABD) + Area of (ΔBDC) =