Find the area of the region enclosed between the two curves x2 + y2 = 9 and (x – 3)2 + y2 = 9.
To find area enclosed by
X2 + y2 = 9 (i)
(x – 3)2 + y2 = 9 (ii)
On solving equation (i) and (ii) we get,
X = ![]() and y = ±
and y = ±![]()
Equation (i) represents a circle with centre (0,0) and meets axes at (±3,0),(0,±3).
Equation (ii) is a circle with centre (3,0) and meets axe at (0,0), (6,0).
They intersect each other at ![]() and
and ![]() .
.
These are shown in the graph below:
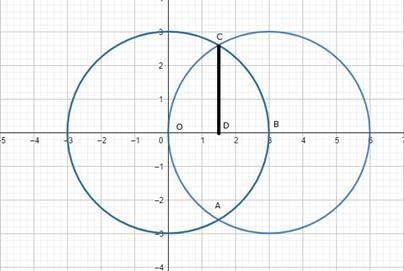
Required area = Region OABCO
= 2(Region OBCO)
= 2(Region ODCO + Region DBCD)
![]()
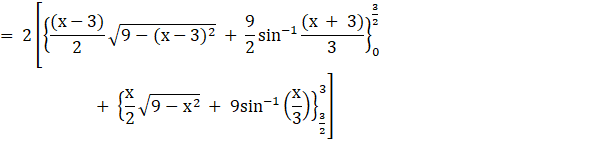
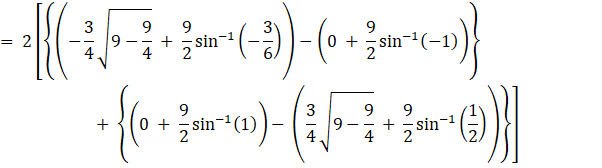
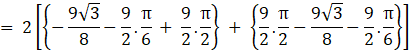
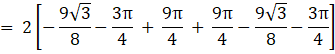
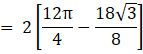
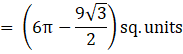
The area of the region enclosed between the two curves curves x2 + y2 = 9 and (x – 3)2 + y2 = 9 is ![]()
42