Find the area of the region {(x,y): x2 + y2 ≤ 4, x + y ≥ 2}
The equation of the given curves are
X2 + y2 = 4 (i)
X + y = 2 (ii)
Clearly X2 + y2 = 4 represents a circle X + y = 2 is the equation of a straight line cutting x and y axes at (0, 2) and (2, 0) respectively.
These are shown in the graph below:
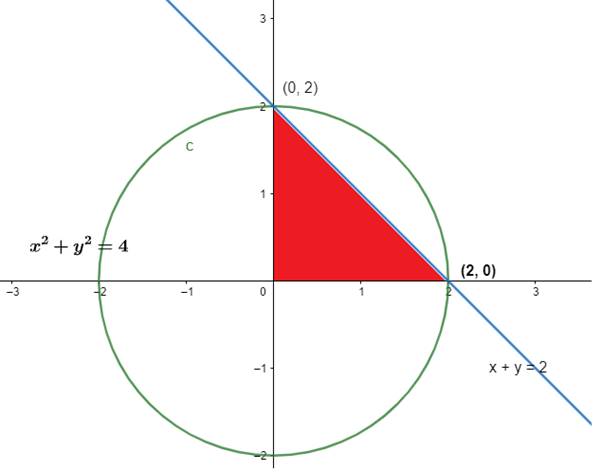
The required area is given by
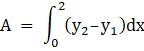
We have y1 = 2 – x and y2 = ![]()
![]()
![]()
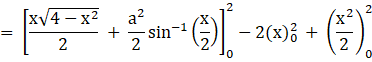
![]()
![]()
![]()
![]()
the area of the region {(x,y): x2 + y2≤ 4, x + y ≥ 2}is ![]()
43