Using integration find the area of the region bounded by the curve , x 2 + y 2 – 4x = 0 and the x-axis.

Question

Philoid · Accepted Answer

First, let us find the intersection points of the curve,

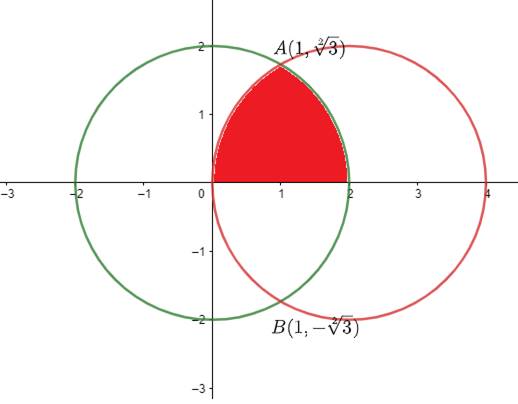
Given Equations are x² + y² = 4 and x² + y² – 4 x = 0.

From both of the equations,

4 x = 4

x = 1

Putting this value in x² + y² = 4, we get,

1 + y² = 4

y² = 3

y = ±√3

Thus the curves intersect at A(1, √3) and B(1, - √3)

The area to be found is shaded in the figure above.

Area of Shaded region =

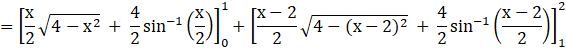
Area of Shaded region = square units.