To find the area of the figure bounded by

y = |x – 1|

Y = x – 1 is a straight line passing through A(1,0)

Y = 1 – x is a straight line passing through A(1,0) and cutting y - axis at B(0,1)

y = 3 – |x|

Y = 3 – x is a straight line passing through C(0,3)and O(3,0)

Y = 3 + x is a straight line passing through C(0,3)and D( – 3,0)

Point of intersection for

Y = x – 1

And y = 3 – x

We get

X – 1 = 3 – x

or, 2x – 4 = 0

or, x = 2

or, y = 2 – 1 = 1

Thus, point of intersection for y = x – 1 and y = 3 + x is B(2,1)

Point of intersection for

y = 1 – x

y = 3 + x

or,1 – x = 3 + x

or, 2x = – 2

or, x = – 1

or, y = 1 – ( – 1) = 2

Thus, point of intersection for y = 1 – x and y = 3 + x is D( – 1,2)

These are shown in the graph below:

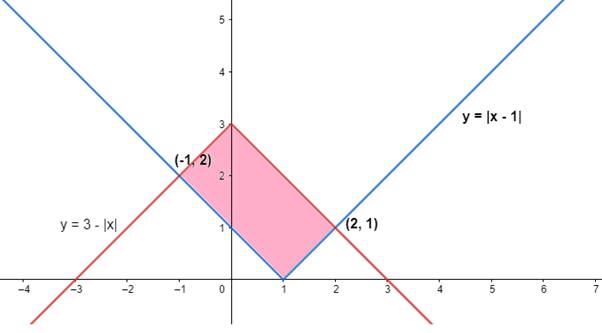
Required area = Region ABCDA

= Region ABFA + Region AFCEA + Region CDEC

The area of the figure bounded by the curves y = |x – 1| and y = 3 – |x| is 4 sq. units