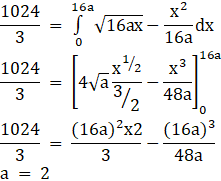If the area enclosed by the parabolas y2 = 16ax and x2 = 16ay, a>0 is 1024/3 square units, find the value of a.
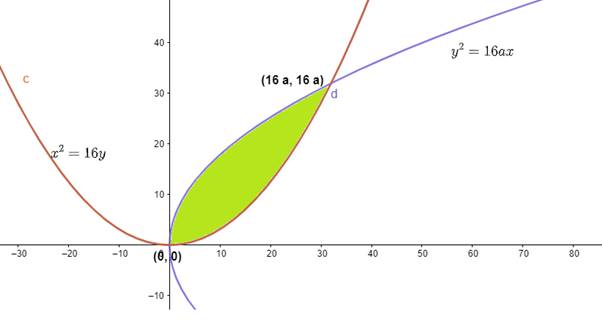
Area of the bounded region - 1024/3
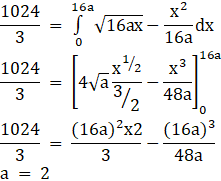
52
If the area enclosed by the parabolas y2 = 16ax and x2 = 16ay, a>0 is 1024/3 square units, find the value of a.

Area of the bounded region - 1024/3