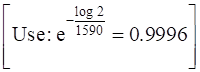
Let the quantity of radium at any time t be A.

According to question,

⇒ where k is a constant

⇒

⇒

Integrating both sides, we have

⇒ ∫ = – k∫dt

⇒ log|A| = – kt + c……(1)

Given, Initial quantity of radium be A₀ when t = 0 sec

Putting the value in equation (1)

∴ log|A| = – kt + c

⇒ log| A₀| = 0 + c

⇒ c = log| A₀| ……(2)

Putting the value of c in equation (1) we have,

log|A| = – kt + log| A₀|

⇒ log|A| – log| A₀| = – k t []

⇒ log ( = – kt ……(3)

Given its half life = 1590 years,

From equation(3),we have

∴ – kt = log (

⇒ – k×1590 = log (

⇒ – k×1590 =

⇒ – k×1590 = – log 2

⇒ k =

∴ The equation becomes

log ( = – t

log ( = – 0.9996 t

Percentage Disappeared = (1 – 0.9996) × 100 = 0.04 %