Find the equation to the curve satisfying 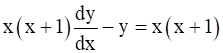 and passing through (1, 0).
and passing through (1, 0).
⇒ ![]()
⇒ ![]()
We can see that it is a linear differential equation.
Comparing it with ![]()
P = – ![]() , Q = 1
, Q = 1
I.F = e∫Pdx
= e![]() dx
dx
= e![]() dx
dx
= elog|x + 1| – log|x|
= elog![]()
= ![]()
Solution of the given equation is given by
y × I.F = ∫Q × I.F dx + c
⇒ y × ![]() = ∫ 1 ×
= ∫ 1 × ![]() dx + c
dx + c
⇒ y × ![]() = ∫
= ∫ ![]() dx + c
dx + c
⇒ y × ![]() = x + logx + c ……(1)
= x + logx + c ……(1)
As the equation passing through (1,0),
0 = 1 + log1 + c
⇒ c = – 1
Putting the value of c in equation (1)
∴ y × ![]() = x + logx – 1
= x + logx – 1
20