Find the area of the triangle formed by joining the mid-points of the sides of the trianglewhose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle

Question

Find the area of the triangle formed by joining the mid-points of the sides of the trianglewhose vertices are (0, &#x2013;1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle

Philoid · Accepted Answer

Let the vertices of the triangle be A (0, - 1), B (2, 1), C (0, 3)

Let D, E, F be the mid-points of the sides of this triangle. Coordinates of D, E, and F are given by

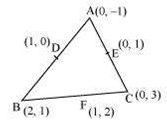
D = (, ) = (1, 0)

E = () = (0, 1)

F = () = (1, 2)

Area of the triangle (DEF) = [1 (2 – 1) + 1(1- 0) + 0 (0- 2)

= (1 + 1)

= 1 square unit

Area of the triangle (ABC) = = [0 (1 – 3) + 2(3+ 1) + 0 (-1- 1)

= * 8

= 4 square units

Therefore, required ratio = 1: 4