Given 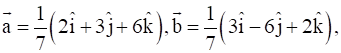
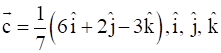 being a right handed orthogonal system of unit vectors in space, show that
being a right handed orthogonal system of unit vectors in space, show that ![]() is also another system.
is also another system.
To show that![]() ,
,![]() ,
,![]() is a right handed orthogonal system of unit vectors, we need to prove the following –
is a right handed orthogonal system of unit vectors, we need to prove the following –
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
Let us consider each of these one at a time.
(a) Recall the magnitude of the vector ![]() is
is
![]()
First, we will find![]() .
.
![]()
![]()
![]()
![]()
Now, we will find![]() .
.
![]()
![]()
![]()
![]()
Finally, we will find![]() .
.
![]()
![]()
![]()
![]()
Hence, we have ![]()
(b) Now, we will evaluate the vector![]()
Recall the cross product of two vectors ![]() and
and ![]() is
is
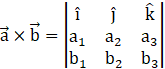
Taking the scalar![]() common, here, we have (a1, a2, a3) = (2, 3, 6) and (b1, b2, b3) = (3, –6, 2)
common, here, we have (a1, a2, a3) = (2, 3, 6) and (b1, b2, b3) = (3, –6, 2)
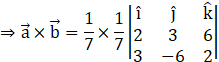
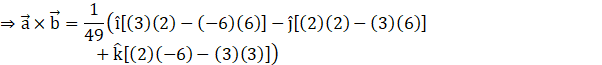
![]()
![]()
![]()
Hence, we have![]() .
.
(c) Now, we will evaluate the vector![]()
Taking the scalar![]() common, here, we have (a1, a2, a3) = (3, –6, 2) and (b1, b2, b3) = (6, 2, –3)
common, here, we have (a1, a2, a3) = (3, –6, 2) and (b1, b2, b3) = (6, 2, –3)
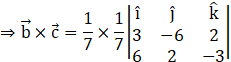
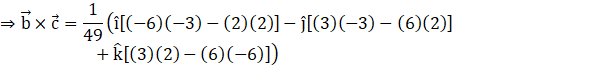
![]()
![]()
![]()
Hence, we have![]() .
.
(d) Now, we will evaluate the vector![]()
Taking the scalar![]() common, here, we have (a1, a2, a3) = (6, 2, –3) and (b1, b2, b3) = (2, 3, 6)
common, here, we have (a1, a2, a3) = (6, 2, –3) and (b1, b2, b3) = (2, 3, 6)
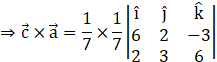
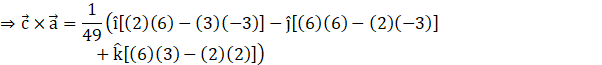
![]()
![]()
![]()
Hence, we have![]() .
.
Thus,![]() ,
,![]() ,
,![]() is also another right handed orthogonal system of unit vectors.
is also another right handed orthogonal system of unit vectors.