We know if either or.

To verify if the converse is true, we suppose

We know the cross product of two vectors and forming an angle θ is

where is a unit vector perpendicular to and .

So, if, we have at least one of the following true –

(a)

(b)

(c) and

(d) is parallel to

The first three possibilities mean that either or or both of them are true.

However, there is another possibility that when the two vectors are parallel. Thus, the converse is not true.

We will justify this using an example.

Given and

Recall the cross product of two vectors and is

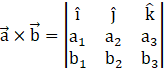
Here, we have (a₁, a₂, a₃) = (1, 3, –2) and (b₁, b₂, b₃) = (2, 6, –4)

Hence, we have even when and.

Thus, the converse of the given statement is not true.