Let ABCD be a square having ( - 1, 2) and (3, 2) as vertices A and C respectively. Let (x, y), (x1, y1) be the coordinate of vertex B and D respectively

We know that the sides of a square are equal to each other

AB = BC

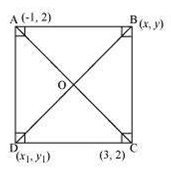
[(x + 1)² + (y - 2)²]^1/2 = [(x - 3)² + (y - 2)²]^1/2

x² + 2x + 1 + y² – 4y + 4 = x² + 9 – 6x + y² + 4 – 4y

8x = 8

x = 1

We know that in a square, all interior angles are of 90°.

In ΔABC,

AB² + BC² = AC²

[(x + 1)² + (y - 2)²]^{1/2 * 2} + [(x - 3)² + (y - 2)²]^{1/2 * 2} = [(3 + 1)² + (2 - 2)²]^{1/2 * 2}

4 + y² + 4 - 4y + 4 + y² - 4y + 4 =16

2y² + 16 - 8 y =16

2y² - 8 y = 0

y(y - 4) = 0

y = 0 or 4

We know that in a square, the diagonals are equal inlength and bisect each other at 90°.

Let O be the mid-point ofAC. Therefore, it will also be the mid-point of BD