ABCD is a parallelogram. The position vectors of the points A, B and C are respectively, and Find the vector equation of the line BD. Also, reduce it to Cartesian form.

Question

Philoid · Accepted Answer

Given: the vectors of point A = , B = and

C =

this means that the vector equation of line AB is given by

where and

so the vector equation of AB is

now the vector equation of BC is given as

where and

therefore the vector equation of BC is given as

The concept of the question:

the vector equation of the diagonal BD is given by

and the vector equation of diagonal AC is given by

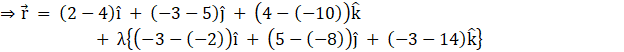
……(1)

can be written as

…..(2)

Comparing 1&2

x = –2–, y = –8 + 13, z = 14–17

Therefore, a cartesian equation of the required line is