Show that the lines 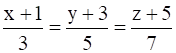 and
and 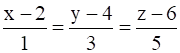 intersect. Find their point of intersection.
intersect. Find their point of intersection.
Given: - Two lines equation:![]() and
and ![]()
To find: - Intersection point
We have,
![]()
⇒ x = 3λ – 1, y = 5λ – 3 and z = 7λ – 5
So, the coordinates of a general point on this line are
(3λ – 1, 5λ – 3, 7λ – 5)
The equation of the 2nd line is
![]()
⇒ x = μ + 2, y = 3μ + 4 and z = 5μ + 6
So, the coordinates of a general point on this line are
(μ + 2, 3μ + 4, 5μ + 6)
If the lines intersect, then they must have a common point.
Therefore for some value of λ and μ, we have
⇒ 3λ – 1 = μ + 2 , 5λ – 3 = 3μ + 4, and 7λ – 5 = 5μ + 6
⇒ ![]() ……(i)
……(i)
⇒ 5λ – 3μ = 7 ……(ii)
and 7λ – 5μ = 11 ……(iii)
putting value of λ from eq i in eq ii, we get
![]()
![]()
![]()
![]()
![]()
Now putting value of μ in eq i, we get
⇒ ![]()
⇒ ![]()
![]()
As we can see by putting the value of λ and μ in eq iii, that it satisfy the equation.
Check
⇒ 7λ – 5μ = 11
⇒ ![]()
⇒ ![]()
⇒ 11 = 11
⇒ LHS = RHS ; Hence intersection point exists or line do intersects
We can find an intersecting point by putting values of μ or λ in any one general point equation
Thus,
Intersection point
3λ – 1, 5λ – 3, 7λ – 5
![]()
![]()