Find the foot of perpendicular from the point (2, 3, 4) to the line 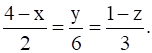 Also, find the perpendicular distance from the given point to the line.
Also, find the perpendicular distance from the given point to the line.
Given: - Point P(2, 3, 4) and the equation of the line ![]()
Let, PQ be the perpendicular drawn from P to given line whose endpoint/ foot is Q point.
Thus to find Distance PQ we have to first find coordinates of Q
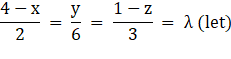
⇒ x = 4 – 2λ, y = 6λ, z = 1 – 3λ
Therefore, coordinates of Q( – 2λ + 4, 6λ, – 3λ + 1)
Now as we know (TIP) ‘if two points A(x1,y1,z1) and B(x2,y2,z2) on a line, then its direction ratios are proportional to (x2 – x1,y2 – y1,z2 – z1)’
Hence
Direction ratio of PQ is
= ( – 2λ + 4 – 2), (6λ – 3), ( – 3λ + 1 – 4)
= ( – 2λ + 2), (6λ – 3), ( – 3λ – 3)
and by comparing with given line equation, direction ratios of the given line are
(hint: denominator terms of line equation)
= ( – 2,6, – 3)
Since PQ is perpendicular to given line, therefore by “condition of perpendicularity.”
a1a2 + b1b2 + c1c2 = 0 ; where a terms and b terms are direction ratio of lines which are perpendicular to each other.
⇒ – 2( – 2λ + 2) + (6)(6λ – 3) – 3( – 3λ – 3) = 0
⇒ 4λ – 4 + 36λ – 18 + 9λ + 9 = 0
⇒ 49λ – 13 = 0
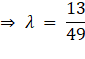
Therefore coordinates of Q
i.e. Foot of perpendicular
By putting the value of λ in Q coordinate equation, we get
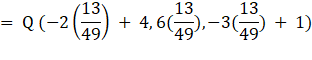
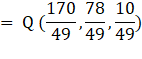
Now,
Distance between PQ
Tip: - Distance between two points A(x1,y1,z1) and B(x2,y2,z2) is given by
![]()
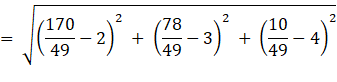
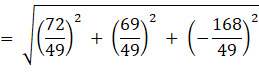
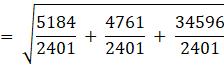
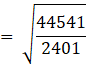
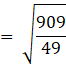
![]() units
units