Find the vector equation of the plane passing through point A(a, 0, 0), B(0, b, 0) and C(0, 0, c). Reduce it to normal form. If plane ABC is at a distance p from the origin, prove that .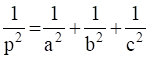

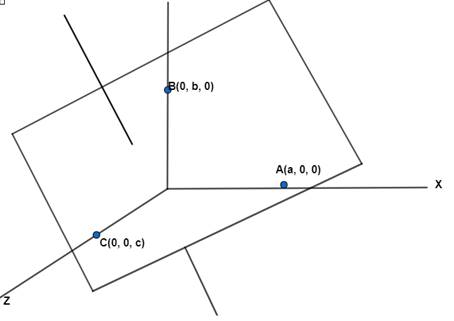
Question

Philoid · Accepted Answer

The required plane passes through the point A(a,0,0) whose position vector is and is normal to the vector given by

Clearly,

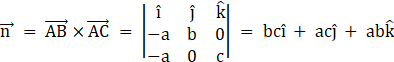
The vector equation of the required plane is,

or,

or, …… (i)

Now,

For reducing (i) to normal form, we need to divide both sides of (i) by

Then, we get,

, which is the normal form of plane (i)

So, the distance of the plane (i) from the origin is,

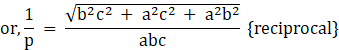
Hence, Proved.