Find the shortest distance between the lines 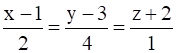 and 3x – y – 2z + 4 = 0 = 2x + y + z + 1.
and 3x – y – 2z + 4 = 0 = 2x + y + z + 1.
Let the two lines be l1 and l2.
So, ![]() and l2: 3x – y – 2z + 4 = 0 = 2x + y + z + 1
and l2: 3x – y – 2z + 4 = 0 = 2x + y + z + 1
We need to find the shortest distance between l1 and l2.
The equation of a plane containing the line l2 is given by
(3x – y – 2z + 4) + λ(2x + y + z + 1) = 0
⇒ (3 + 2λ)x + (λ – 1) y + (λ – 2) z + (4 + λ) = 0
Direction ratios of l1 are 2, 4, 1 and those of the line containing the shortest distance are proportional to 3 + 2λ, λ – 1 and λ – 2.
We know that if two lines with direction ratios (a1, b1, c1) and (a2, b2, c2) are perpendicular to each other, then a1a2 + b1b2 + c1c2 = 0.
⇒ (3 + 2λ)(2) + (λ – 1)(4) + (λ – 2)(1) = 0
⇒ 6 + 4λ + 4λ – 4 + λ – 2 = 0
⇒ 9λ = 0
∴ λ = 0
Thus, the plane containing line l2 is 3x – y – 2z + 4 = 0.
We have![]()
When α = 0, (x, y, z) = (1, 3, –2)
So, the point (1, 3, –2) lies on the line l1.
Hence, the shortest distance between the two lines is same as the distance of the perpendicular from (1, 3, –2) on to the plane 3x – y – 2z + 4 = 0.
Recall the length of the perpendicular drawn from (x1, y1, z1) to the plane Ax + By + Cz + D = 0 is given by
![]()
Here, (x1, y1, z1) = (1, 3, –2) and (A, B, C, D) = (3, –1, –2, 4)
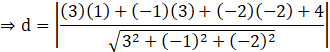
![]()
![]()
![]()
Thus, the required shortest distance is![]() units.
units.