Let point P = (3, 2, 1) and M be the image of P in the plane 2x – y + z + 1 = 0.

In addition, let Q be the foot of the perpendicular from P on to the given plane so that Q is the midpoint of PM.

Direction ratios of PM are proportional to 2, –1, 1 as PM is normal to the plane.

Recall the equation of the line passing through (x₁, y₁, z₁) and having direction ratios proportional to l, m, n is given by

Here, (x₁, y₁, z₁) = (3, 2, 1) and (l, m, n) = (2, –1, 1)

Hence, the equation of PM is

⇒ x = 2α + 3, y = 2 – α, z = α + 1

Let M = (2α + 3, 2 – α, α + 1).

Now, we will find Q, the midpoint of PM.

Using the midpoint formula, we have

This point Q lies on the given plane, which means Q satisfies the plane equation 2x – y + z + 1 = 0.

We have M = (2α + 3, 2 – α, α + 1)

⇒ M = (2(–2) + 3, 2 – (–2), (–2) + 1)

∴ M = (–1, 4, –1)

We have

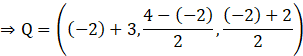
∴ Q = (1, 3, 0)

Using the distance formula, we have

Thus, the required foot of perpendicular is (1, 3, 0) and the length of the perpendicular is units. Also, the image of the given point is (–1, 4, –1)