Let C be the set of all complex numbers and C0 be the set of all non-zero complex numbers. Let a relation R on C0 be defined as
z1 R z2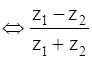 is real for all z1, z2∈ C0.
is real for all z1, z2∈ C0.
Show that R is an equivalence relation.
We have,
![]()
We want to prove that R is an equivalence relation on Z.
Now,
Proof :
To prove that relation is equivalence, we need to prove that it is reflexive, symmetric and transitive.
Reflexivity : For Reflexivity, we need to prove that-
(a, a) ∈ R
Let a ∈ C0
![]()
And, 0 is real
∴ (a, a) ∈ R, so R is reflexive
Symmetric: For Symmetric, we need to prove that-
If (a, b) ∈ R, then (b, a) ∈ R
Let (a, b) ∈ R
![]()
⇒ p is real.
![]()
And ∵ p is real
⇒ -p is also a real no.
⇒ (b, a) ∈ R, so R is symmetric
Transitive : : For Transitivity, we need to prove that-
If (a, b) ∈ R and (b, c) ∈ R, then (a, c) ∈ R
Let (a, b) ∈ R and (b, c) ∈ R
![]()
⇒ p is real no.
![]()
![]()
![]() ….(1)
….(1)
![]()
⇒ q is real.
![]()
![]()
![]() …..(2)
…..(2)
Dividing (1) by (2), we get-
![]()
Where, Q is a rational number.
⇒ Q is real number
Now, by componendo dividendo-
![]()
⇒ (a, c) ∈ R.
⇒ R is transitive
Thus, R is reflexive, symmetric and, transitive on C0.
Hence, R is an equivalence relation on C0.