Given:- Rhombus OABC i.e all sides are equal

To Prove:- Diagonals are perpendicular bisector of each other

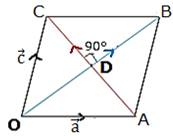
Proof:- Let, O at the origin

D is the point of intersection of both diagonals

be position vector of A and C respectively

Then,

Now,

⇒

as AB = OC

⇒ ……(i)

Similarly

⇒

⇒ ……(ii)

Tip:- Directions are important as sign of vector get changed

Magnitude are same AC = OB = √a² + c²

Hence from two equations, diagonals are equal

Now let’s find position vector of mid-point of OB and AC

⇒

⇒

and

⇒

⇒

Magnitude is same AD = DC = OD = DB = 0.5(√a² + c²)

Thus the position of mid-point is same, and it is the bisecting point D

By Dot Product of OB and AC vectors we get,

⇒

⇒

⇒

⇒

As the side of a rhombus are equal OA = OC

⇒

⇒

Hence OB is perpendicular on AC

Thus diagonals of rhombus bisect each other at 90°