Given:- ΔABC, AD is median

To Prove:- If AD is perpendicular on base BC then ΔABC is isosceles

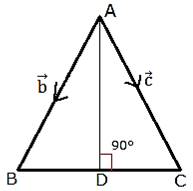
Proof:- Let, A at Origin

be position vector of B and C respectively

Therefore,

Now position vector of D, mid-point of BC i.e divides BC in 1:1

Section formula of internal division: Theorem given below

“Let A and B be two points with position vectors

respectively, and c be a point dividing AB internally in the ration m:n. Then the position vector of c is given by

Position vector of D is given by

⇒

Now distance/length of BC

= position vector of C-position vector of B

⇒

Now, assume median AD is perpendicular at BC

Then by Dot Product

⇒

⇒

⇒

⇒

⇒

⇒ AC = AB

Thus two sides of ΔABC are equal

Hence ΔABC is isosceles triangle