Given: - Two curves are y² = 4x and y = 2x – 4

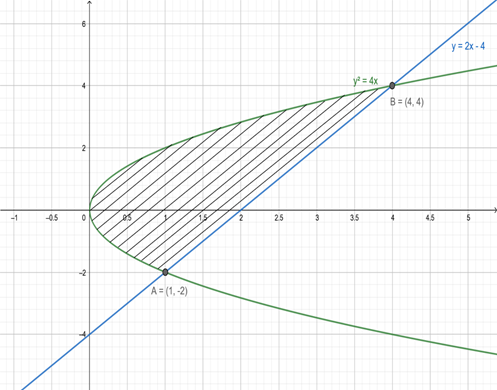
Now to find the area between these two curves, we have to find common area i.e. Shaded portion

Intersection of parabola y² = 4x with line y = 2x – 4

Putting the value of y from the equation of a line in parabola equation, we get,

y² = 4x

⇒ (2x – 4)² = 4x

⇒ 4x² – 16x + 16 = 4x

⇒ 4x² – 20x + 16 = 0

⇒ 4x² – 16x – 4x + 16 = 0

⇒ 4x(x – 4) – 4(x – 4) = 0

⇒ 4(x – 1)(x – 4) = 0

⇒ (x – 1)(x – 4) = 0

⇒ x = 1,4

When x = 1, y = √4x

⇒ y = + 2, – 2; we take – 2 as the intersection is in the 4^th quadrant and when x = 4, y = √4x

⇒ y = + 4, – 4; we take + 4 as the intersection is in 1^st quadrant

Therefore intersection points are B(4,4) and C(1, – 2)

Area of the bounded region, taking strips

i) By using horizontal strips

Therefore, limits are for y and integrating with respect to y

Area bounded by region = {Area under line from – 2 to 4} –{Area under parabola from – 2 to 4}

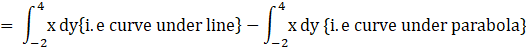
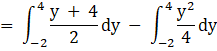
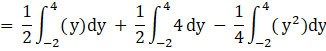
Putting limits, we get

ii) By using vertical strips.

Therefore, limits are for x, and integrating with respect to x

Area bounded by region = {2(Area under parabola from 0 to 1) + (Area under parabola from 1 to 4)} – {Area under line from 1 to 4}

Tip: - Parabola is symmetrical about x - axis therefore its area is twice the area above x - axis. So, till its latus rectum i.e here a = 1, area is twice the area above x - axis.

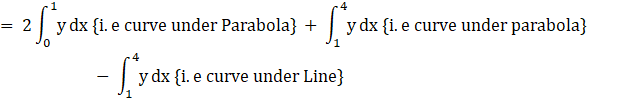
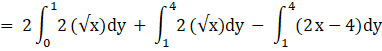
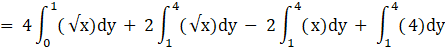
Putting limits, we get,

Hence from both methods we get same answer