Given: -

Two equation;

Parabola y^{2 =} 2x and

Line x – y = 4

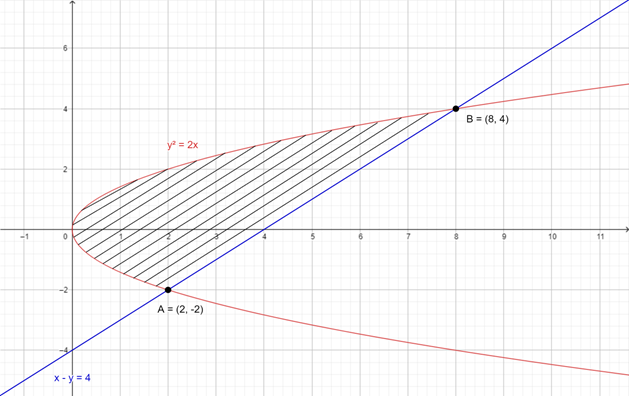
Now to find an area between these two curves, we have to find a common area or the shaded part.

From figure we can see that,

Area of shaded portion = Area under line curve – Area under parabola; horizontal strip

Now, Intersection points;

From parabola and line equation equate y, x – 4 = y we get

⇒ y² = 2x

⇒ (x – 4)^{2 =} 2x

⇒ x² – 8x + 16 = 2x

⇒ x² – 10x + 16 = 0

⇒ x² – 8x – 2x + 16 = 0

⇒ x(x – 8) – 2(x – 8) = 0

⇒ (x – 8)(x – 2) = 0

⇒ x = 8,2

So, by putting the value of x in any curve equation, we get,

⇒ y = x – 4

For x = 8

⇒ y = 8 – 4

⇒ y = 4

For x = 2

⇒ y = 2 – 4

⇒ y = – 2

Therefore, two intersection points coordinates are (8, 4) and (2, – 2)

Area of the bounded region

= Area under the line curve from – 2 to 4 – Area under parabola from – 2 to 4

Tip: - Take limits as per strips. If the strip is horizontal than take y limits or if integrating with respect to y then limits are of y.

Area bounded by region = {Area under line from – 2 to 4} – {Area under parabola from – 2 to 4}

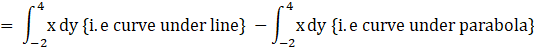
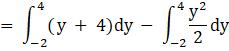
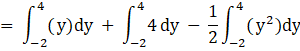
Putting limits, we get

= 6 + 24 – 12

= 18 sq units