Classify the following functions as injection, surjection or bijection:
f: Q – {3} → Q, defined by 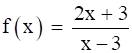
TIP: – One – One Function: – A function ![]() is said to be a one – one functions or an injection if different elements of A have different images in B.
is said to be a one – one functions or an injection if different elements of A have different images in B.
So, ![]() is One – One function
is One – One function
⇔ a≠b
⇒ f(a)≠f(b) for all ![]()
⇔ f(a) = f(b)
⇒ a = b for all ![]()
Onto Function: – A function ![]() is said to be a onto function or surjection if every element of A i.e, if f(A) = B or range of f is the co – domain of f.
is said to be a onto function or surjection if every element of A i.e, if f(A) = B or range of f is the co – domain of f.
So, ![]() is Surjection iff for each
is Surjection iff for each ![]() , there exists
, there exists ![]() such that f(a) = b
such that f(a) = b
Bijection Function: – A function ![]() is said to be a bijection function if it is one – one as well as onto function.
is said to be a bijection function if it is one – one as well as onto function.
Now, f : R → R given by ![]()
Check for Injectivity:
Let x,y be elements belongs to Q i.e ![]() such that
such that
⇒ f(x) = f(y)
⇒ ![]()
⇒ (2x + 3)(y – 3) = (2y + 3)(x – 3)
⇒ 2xy – 6x + 3y – 9 = 2xy – 6y + 3x – 9
⇒ – 6x + 3y = – 6y + 3x
⇒ – 6x + 3y + 6y – 3x = 0
⇒ – 9x + 9y = 0
⇒ x = y
Thus, f is One – One function
Check for Surjectivity:
Let y be element belongs to Q i.e ![]() be arbitrary, then
be arbitrary, then
⇒ f(x) = y
⇒ ![]()
⇒ 2x + 3 = y (x – 3)
⇒ 2x + 3 = xy – 3y
⇒ 2x – xy = – 3(y + 1)
⇒ ![]()
Above value of x belongs to Q – [3] for y = 2
Therefore for each element in Q – [3] (co – domain), there does not exist an element in domain Q.
Hence, f is not onto function
Thus, Not Bijective function