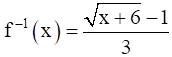We have f : R⁺→ [–5, ∞) and f(x) = 9x² + 6x – 5.

Recall that a function is invertible only when it is both one-one and onto.

First, we will prove that f is one-one.

Let x₁, x₂ϵ R⁺ (domain) such that f(x₁) = f(x₂)

⇒ 9x₁² + 6x₁ – 5 = 9x₂² + 6x₂ – 5

⇒ 9x₁² + 6x₁ = 9x₂² + 6x₂

⇒ 9x₁² – 9x₂² + 6x₁ – 6x₂ = 0

⇒ 9(x₁² – x₂²) + 6(x₁ – x₂) = 0

⇒ 9(x₁ – x₂)(x₁ + x₂) + 6(x₁ – x₂) = 0

⇒ (x₁ – x₂)[9(x₁ + x₂) + 6] = 0

⇒ x₁ – x₂ = 0 (as x₁, x₂ϵ R⁺)

∴ x₁ = x₂

So, we have f(x₁) = f(x₂) ⇒ x₁ = x₂.

Thus, function f is one-one.

Now, we will prove that f is onto.

Let y ϵ [–5, ∞) (co-domain) such that f(x) = y

⇒ 9x² + 6x – 5 = y

Adding 6 to both sides, we get

9x² + 6x – 5 + 6 = y + 6

⇒ 9x² + 6x + 1 = y + 6

⇒ (3x + 1)² = y + 6

Clearly, for every y ϵ [4, ∞), there exists x ϵ R⁺ (domain) such that f(x) = y and hence, function f is onto.

Thus, the function f has an inverse.

We have f(x) = y ⇒ x = f^-1(y)

But, we found f(x) = y ⇒

Hence,

Thus, f(x) is invertible and