Prove that the operation * on the set
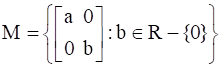 defined by A*B=AB is a binary operation.
defined by A*B=AB is a binary operation.
Given that * is an operation that is valid on the set 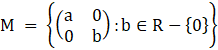 and it is defined as given:A*B = A B.
and it is defined as given:A*B = A B.
According to the problem it is given that on applying the operation * for two given numbers in the set ‘M’ it gives a number in the set ‘M’ as a result of the operation.
⇒ A*B∈M ...... (1)
Let us take ![]() here a∈R, b∈R, c∈R and d∈R then,
here a∈R, b∈R, c∈R and d∈R then,
⇒ ![]()
⇒ 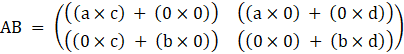
⇒ ![]()
⇒ ![]()
Since a∈R and c∈R then ac∈R
And also b∈R and d∈R then bd∈R.
⇒ AB∈R
∴ The operation ‘*’ defines a binary operation on ‘M’.
7