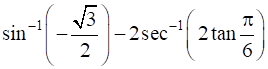
Let,

sin^{–1 =} y

⇒ sin y =

⇒ –sin y =

⇒ –sin

As we know sin(–θ) = –sinθ

∴ –sin = sin

The range of principal value of sin^–1 is and sin

Therefore, the principal value of sin^–1 is ….(1)

Let us assume 2tan = θ

We know tan

∴ 2tan = 2

⇒ 2tan =

∴ The question converts to sec^–1

Now,

Let sec^–1 = z

⇒ sec z =

= sec

The range of principal value of sec^–1is [0, π]–{}

and sec

Therefore, the principal value of sec^–1(2tan) is …..(2)

∴ Sin^–1 – 2sec^–1(2tan)

= – (from (1) and (2))

=

= –π

Therefore, the value of Sin^–1 – 2sec^–1(2tan) is –π.